
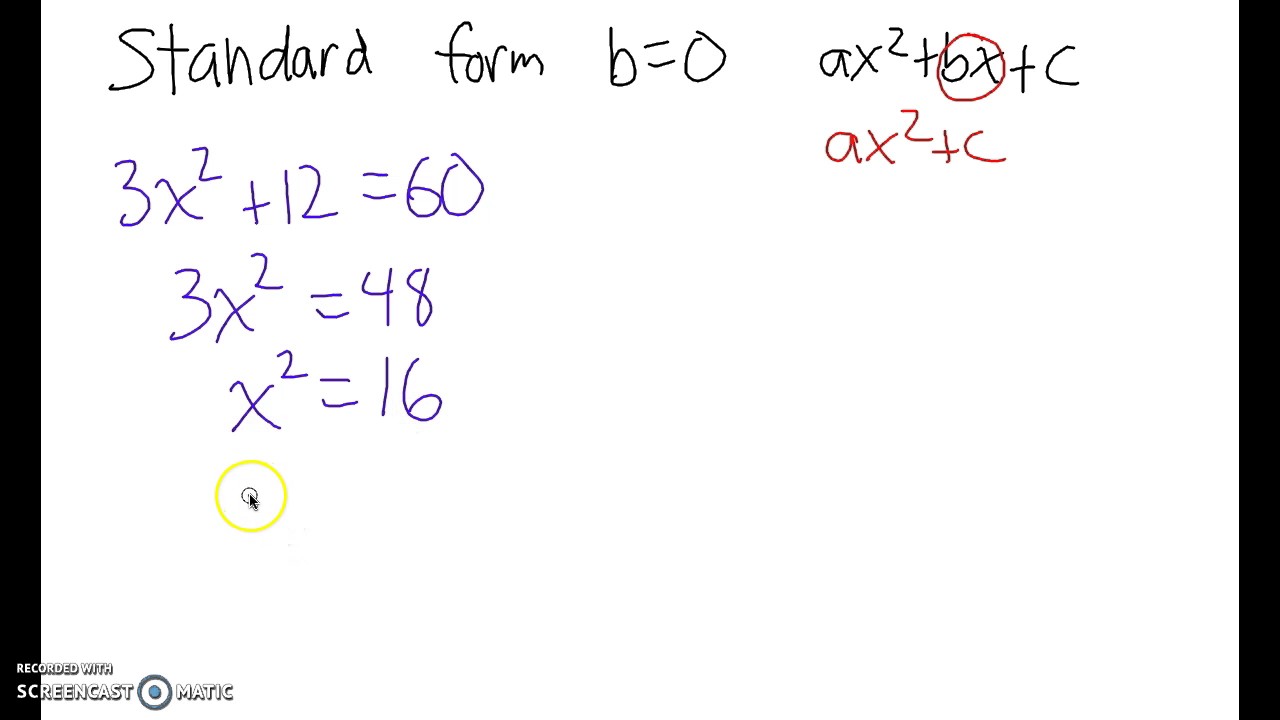
Therefore for this equation, there are no real number solutions. There is no real number whose square is negative. We say this because the root of a negative number can’t be any real number. Hence, the nature of the roots α and β of equation ax2 + bx + c = 0 depends on the quantity or expression (b2 – 4ac) under the square root sign. The formulas for solving quadratic equations can be write as: Let α and β be the roots of quadratic equation in the general form: ax2 + bx + c = 0.

The number of roots of a polynomial equation is equal to its degree. The value of a variable for which the equation gets satisfied is called the solution or the root of quadratic equation. Students often wonder if a quadratic equation can have more than one solution? Are there any equations that don’t have any real solution? Yes, it’s possible with the root of quadratic equation concept. Using the quadratic equation formula, x = (−2 ± √0)/2 = −2/2ĭownload the Quadratic Equation Cheat Sheet online Here’s an example that will give you an understanding on what it takes while solving quadratic equations. The quantity in the square root is called the discriminant or D. Just plug in the values of a, b and c, and do the calculations. If ax 2 + bx + c = 0 is a quadratic equation, then the value of x is given by the following formula: Below-mentioned is the general quadratic equation formula. Quadratic Equation Formula/ Formulas for Solving Quadratic Equationsįormulas for solving quadratic equations provide students with requisite knowledge to deal with complex numericals easily. In 12th century, Spain, a Jewish mathematician Abraham bar Hiyya Ha-Nasi authored the first European book that included a complete solution to the general quadratic equation and finally in 1637, René Descartes, published La Géométrie that contained all the quadratic equation formula that we know today. Over time, various historians kept innovating new ways of finding new formulas for solving quadratic equations. It’s a known fact that mathematicians from Babylonia, Egypt, Greece, China, and India used geometric methods to solve quadratic equations. When we take a peek into the history, practical applications of quadratic equations are dated way back, as early as 2050 BC. Therefore, they are also called “Equations of degree 2”. The word quadratic in the term Quadratic equations is derived from quadratus, a Latin word for ‘square.’ Hence, we define quadratic equations as equations where the variable is of the second degree.


 0 kommentar(er)
0 kommentar(er)
